In this article, we are going to review Invariant tests for AMM contracts with Echidna, with a short comparison with Foundry invariant testing and a deep dive into property-based invariant tests for an Automated Market Maker smart contract.

Introduction

What is Echidna?

Echidna is a smart contract fuzzer. It differs from traditional testing tools by focusing on property-based testing. In this context, properties are invariants or rules a contract should always adhere to, regardless of the state or inputs it receives.

What is our goal in this article?

We want to start using Echidna to write tests in a project with an existing AMM smart contract that we have created.

For those of you who don’t have it configured yet, check out this article (Introduction to Echidna) to set up your environment and then we will start with the invariant test implementation for the SimpleAMM.sol contract.

Echidna vs Foundry Invariant Testing

Echidna’s fuzzing and property-based approach provides a broader, more randomized testing landscape, potentially uncovering a wider range of vulnerabilities, especially edge cases and complex scenarios.

In contrast, Foundry offers a more controlled and precise testing environment, ideal for thoroughly validating known behaviors and specific contract functions.

Let’s go through three main differences:

Input Generation: Echidna’s use of fuzzing for random input generation contrasts with Foundry’s approach of using predefined inputs. This means Echidna can potentially uncover issues that might not be explicitly tested for in Foundry’s more controlled scenarios.
Testing Philosophy: Echidna’s property-based testing, which checks that invariants hold under all conditions, is different from Foundry’s approach to testing specific scenarios and functions. Echidna’s method is more about ensuring overall contract robustness, while Foundry’s is about verifying known behaviors.
Exploration of Edge Cases:
Echidna’s ability to automatically explore a wide range of states and inputs, including edge cases, contrasts with Foundry’s need for manual definition of these scenarios.

Defining the SimpleAMM contract and its invariants

Identifying invariants in a smart contract project typically involves a thorough review of various components of the project, including the code, documentation, and the broader context of the contract’s functionality.

In our case, we are going to extract the invariants from the code we have implemented and from the knowledge we have of Automated Market Makers (AMM).

Here is the SimpleAMM.sol contract we are going to use:

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;

contract SimpleAMM {
    uint256 public constant MINIMUM_RESERVE_THRESHOLD = 500;

    uint256 public reserveTokenA;
    uint256 public reserveTokenB;
    uint256 public constantProduct;

    event LiquidityAdded(
        address indexed user,
        uint256 tokenAAmount,
        uint256 tokenBAmount
    );
    event LiquidityRemoved(
        address indexed user,
        uint256 tokenAAmount,
        uint256 tokenBAmount
    );
    event TokensSwapped(
        address indexed user,
        uint256 tokenASwapped,
        uint256 tokenBReceived
    );
    event TokensToSwap(
        uint256 indexed tokenAToSwapp,
        uint256 indexed tokenBToReceive
    );

    function addLiquidity(uint256 tokenAAmount, uint256 tokenBAmount) public {
        require(
            tokenAAmount > 0 && tokenBAmount > 0,
            "Cannot add zero liquidity"
        );
        reserveTokenA += tokenAAmount;
        reserveTokenB += tokenBAmount;
        updateConstantProduct();
        emit LiquidityAdded(msg.sender, tokenAAmount, tokenBAmount);
    }

    function removeLiquidity(
        uint256 tokenAAmount,
        uint256 tokenBAmount
    ) public {
        require(
            reserveTokenA >= tokenAAmount && reserveTokenB >= tokenBAmount,
            "Insufficient liquidity"
        );
        reserveTokenA -= tokenAAmount;
        reserveTokenB -= tokenBAmount;

        // Check final reserves after swap
        require(
            reserveTokenA >= MINIMUM_RESERVE_THRESHOLD,
            "Reserve Token A below minimum threshold"
        );
        require(
            reserveTokenB >= MINIMUM_RESERVE_THRESHOLD,
            "Reserve Token B below minimum threshold"
        );

        updateConstantProduct();
        emit LiquidityRemoved(msg.sender, tokenAAmount, tokenBAmount);
    }

    function swapTokenAForTokenB(uint256 tokenAAmount) public {
        uint256 tokenBAmount = getSwapAmount(tokenAAmount);
        emit TokensToSwap(tokenAAmount, tokenBAmount);

        require(reserveTokenB >= tokenBAmount, "Insufficient token B reserve");
        reserveTokenA += tokenAAmount;
        reserveTokenB -= tokenBAmount;

        // Check final reserves after swap
        require(
            reserveTokenA >= MINIMUM_RESERVE_THRESHOLD,
            "Reserve Token A below minimum threshold"
        );
        require(
            reserveTokenB >= MINIMUM_RESERVE_THRESHOLD,
            "Reserve Token B below minimum threshold"
        );

        updateConstantProduct();
        emit TokensSwapped(msg.sender, tokenAAmount, tokenBAmount);
    }

    function getSwapAmount(uint256 tokenAAmount) public view returns (uint256) {
        uint256 newReserveA = reserveTokenA + tokenAAmount;
        require(newReserveA > 0, "Invalid swap amount");
        uint256 newReserveB = constantProduct / newReserveA;
        return reserveTokenB - newReserveB;
    }

    function updateConstantProduct() private {
        constantProduct = reserveTokenA * reserveTokenB;
    }
}

Now, let’s list the Invariants that we could extract for this AMM contract and that we are going to use to write our invariant tests:

Constant Product Invariant
Reserve Non-Negativity
Swap Rate Fairness
Liquidity Addition and Removal Consistency
No Token Creation or Destruction
Positive Liquidity
Swap Amount Validation
Solvency

Writing Echidna Tests for the defined Invariants

When implementing invariant tests with Echidna, the tests are typically written directly in Solidity, much like traditional unit tests, but with a focus on the specific properties or invariants you want to ensure hold true for your smart contract.

A few things to consider before starting to write them regarding format:

Naming Convention:
Echidna test files’ naming convention is similar to other Solidity files but often include a specific identifier in the name to indicate they are Echidna tests. In our case, EchidnaSimpleAMM.sol.
Echidna Test Functions: Within this contract, write functions that define your invariants. These functions should return a boolean value, typically true when the invariant holds.
Naming Test Functions: Test function names often start with echidna_ to indicate their purpose.

Let’s start writing our tests:

1. Constant Product Invariant

We need to write a Solidity function that checks whether the product of reserveTokenA and reserveTokenB is always equal to constantProduct after any operation such as adding/removing liquidity or swapping tokens.

Echidna test invariant implementation: (since this is the first test, we will show how the contract should look like, in the next ones we will just add the test)

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;

import "./SimpleAMM.sol";

contract EchidnaSimpleAMM is SimpleAMM {

    constructor() {
       addLiquidity(1000, 1000);
    }

    // Constant Product Invariant
    function echidna_constant_product_invariant() public returns (bool) {
      uint256 product = reserveTokenA * reserveTokenB;
      return product == constantProduct;
    }
}

Now we want to run the test with the command:
echidna . --contract EchidnaSimpleAMM

And then you get, both, the response in the command line and the report:

➜  SimpleAMM git:(master) ✗ echidna . --contract EchidnaSimpleAMM
[...] Compiling .... Done! (0.69665s)
Analyzing contract: ../SimpleAMM/src/EchidnaSimpleAMM.sol:EchidnaSimpleAMM
[2023-12-10 11:44:34.39] Running slither on .... Done! (0.385071s)
echidna_constant_product_invariant: passing

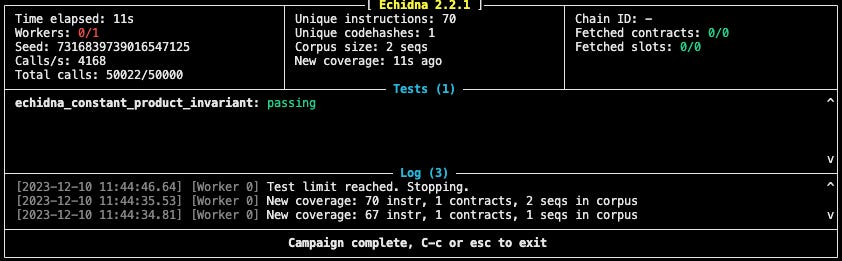
Not to stop here analyzing all the details we get in this output report, we will be explaining each of them as we go.

2. Reserve Non-Negativity

We need to write a Solidity function that checks whether the reserves reserveTokenA and reserveTokenB never become negative after any operation.

Given that Solidity uses unsigned integers (uint256) for these reserves, they inherently cannot be negative. However, it's still good practice to assert this explicitly, as it can help catch underflows or other unexpected behaviors.

Echidna test invariant implementation:

function echidna_test_reserve_non_negativity() public returns (bool) {
    return reserveTokenA >= 0 && reserveTokenB >= 0;
}

Report

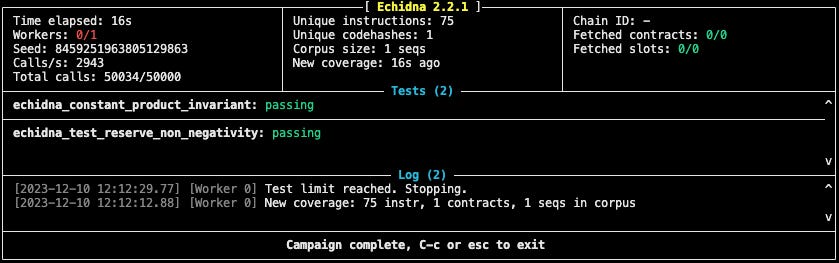
Let’s analyze what the details on the first column from the left indicate:

Time elapsed: The total length it’s taken to run all existing tests
Workers:
It refers to the number of parallel worker processes that Echidna is using to run the tests. Echidna can use multiple threads or processes to execute tests in parallel, which can significantly speed up the testing process, especially for complex contracts or extensive test suites.
Seed: The specific value of the seed is important for reproducibility. If you encounter a particular bug or issue while testing with Echidna, using the same seed value allows you to reproduce the exact sequence of inputs that led to that issue. This is essential for debugging and fixing vulnerabilities in your contract.
Calls/Total calls: They are useful indicators of the testing process’s intensity and coverage. They help you understand how thoroughly your smart contract is being tested and whether the testing is aligning with your configured parameters.

3. Swap Rate Fairness

Now we need to check that the rate at which tokens are swapped remains fair and consistent with the constant product formula. Since the constant product should remain (approximately) the same after swaps, this invariant can be tested by comparing the product of reserves before and after a swap operation.

Echidna test invariant implementation:

function echidna_test_swap_rate_fairness() public returns (bool) {
    uint256 currentProduct = reserveTokenA * reserveTokenB;

    // Allow for a small tolerance due to integer division rounding
    uint256 tolerance = initialConstantProduct / 1000; // Adjust the tolerance as needed

    return (currentProduct >= initialConstantProduct - tolerance) &&
           (currentProduct <= initialConstantProduct + tolerance);
}

After running the tests again, let’s analyze the next details from the report:

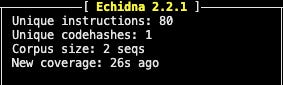
Unique instructions: It indicates the number of unique EVM instructions executed during the fuzz testing process. In our report, “Unique instructions: 80” means that Echidna encountered and executed 80 distinct EVM instructions while testing our smart contract.
Unique codehashes: Each Ethereum smart contract has a unique identifier known as a codehash, which is essentially the hash of the compiled bytecode of the contract. It uniquely represents the contract’s code.
This means that during the fuzz testing process, Echidna encountered and tested only one unique version of the contract’s bytecode.
Corpus size: A corpus in fuzz testing is essentially a collection of inputs or data sets that are used to test the contract. Each sequence in the corpus represents a particular set of transactions or function calls that Echidna uses to interact with our contract.
New coverage: It is indicative of how the current fuzz testing session has expanded the code coverage of your smart contract compared to previous sessions.

4. Liquidity Addition and Removal Consistency

We need to write a function that tests whether adding liquidity to and then removing the same amount from your SimpleAMM contract leaves the reserve balances unchanged.

This function will simulate the process of adding and removing liquidity and then assert that the reserves are consistent with their initial state.

Echidna test invariant implementation:

function echidna_test_liquidity_addition_removal_consistency() public returns (bool) {
    uint256 initialReserveTokenA = reserveTokenA;
    uint256 initialReserveTokenB = reserveTokenB;

    // Add liquidity
    addLiquidity(500, 500);
    // Remove the same amount of liquidity
    removeLiquidity(500, 500);

    // Check if reserves are back to their initial state
    return (reserveTokenA == initialReserveTokenA) &&
        (reserveTokenB == initialReserveTokenB);
}

We now run our tests, and let’s analyze the next details from the report:

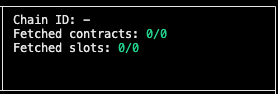
Chain ID: Echidna creates an isolated environment for fuzz-testing smart contracts. Since it’s not interacting with an actual Ethereum network, the Chain ID is not set
Fetched contracts: This parameter typically indicates how many contracts Echidna has loaded from the blockchain for testing purposes. If the report shows “0/0”, it suggests that no on-chain contracts were loaded for testing.
Fetched slots: If you’re testing a contract that is not yet deployed on-chain, Echidna will not fetch or interact with any on-chain storage slots. Therefore, “0/0” fetched slots is an expected outcome.

5. No Token Creation or Destruction

We need to ensure that the total supply of tokens remains constant throughout all operations. This means that the sum of tokens in the reserves and tokens held by users should always equal the initial total supply.

Echidna test invariant implementation:

function echidna_test_token_conservation() public returns (bool) {
    uint256 initialTotalSupply = 100000; // This is a hardcoded value. Simplifying it for the sake of testing.
    uint256 totalReserve = reserveTokenA + reserveTokenB;
    uint256 totalHeldByUsers = 98000; // This is a hardcoded value. Simplifying it for the sake of testing.

    // The total supply should always be equal to the sum of reserves and tokens held by users
    return initialTotalSupply == (totalReserve + totalHeldByUsers);
}

6. Positive Liquidity

We need to verify that the SimpleAMM contract does not allow the addition of zero liquidity. This means ensuring that both tokenAAmount and tokenBAmount in the addLiquidity function must be greater than zero for the operation to succeed.

We will structure the test to try to add zero liquidity and assert that such attempts fail.

Echidna test invariant implementation:

function echidna_test_positive_liquidity() public returns (bool) {
    // Attempt to add zero liquidity
    try addLiquidity(0, 0) {
        // If the call succeeds, return false (test should fail)
        return false;
    } catch {
        // If the call fails, return true (test should pass)
        return true;
    }
}

7. Swap Amount Validation

We need to ensure that the amount returned by the getSwapAmount function is always less than or equal to the current reserveTokenB when swapping Token A for Token B.

This test will help confirm that the swap calculations in the SimpleAMM contract stay within the bounds of available reserves, adhering to the contract's intended logic.

Echidna test invariant implementation:

First, we need to add a state variable

uint256 public tokenAAmount;

The reason to declare it as a state variable and not as a local variable in the test function is that declaring tokenAAmount as a public variable, Echidna will automatically assign random values to it for each test run.

So, here is the invariant test function:

function echidna_test_swap_amount_validation() public returns (bool) {
    // Get the current reserve of Token B
    uint256 currentReserveB = reserveTokenB;

    // Get the swap amount for Token A
    uint256 swapAmountB = getSwapAmount(tokenAAmount); // Where tokenAAmount is randomized by Echidna

    // Check if the swap amount is less than or equal to the reserve of Token B
    return swapAmountB <= currentReserveB;
}

8. Solvency

We need to ensure that after any swap operation, the SimpleAMM contract remains solvent. This means the reserves must always be sufficient to satisfy the constant product formula.

The test will check that the product of the reserves remains constant (within a reasonable tolerance due to integer division) after each swap operation.

Echidna test invariant implementation:

function echidna_test_solvency() public returns(bool) {
    // Swap amount of Token A for Token B
    swapTokenAForTokenB(tokenAAmount); // Where tokenAAmount is randomized by Echidna

    // Check if reserves are still above the minimum allowed threshold
    bool isSolvencyMaintained = (reserveTokenA >= MINIMUM_RESERVE_THRESHOLD) &&
                                (reserveTokenB >= MINIMUM_RESERVE_THRESHOLD);

    return isSolvencyMaintained;
}

Final result

This is it, for now, we have 8 property-based invariant tests that are already increasing the security of our code. Make sure to stay around because soon we will be diving deeper into invariant tests with Echidna.

Conclusion

Through this article, we've extensively explored how to apply Echidna for invariant testing within the context of Automated Market Makers. By defining critical invariants and implementing rigorous tests, we ensure that the smart contract adheres to its foundational logic under all circumstances.

The detailed comparison with Foundry testing methods underscores Echidna's unique ability to identify potential vulnerabilities, providing a robust framework for safeguarding blockchain implementations against a variety of risks.

As smart contract complexity grows, such sophisticated testing is not just beneficial; it's necessary to maintain the trustworthiness and security of decentralized applications.

Zealynx Security